The Pythagorean Theory of Music and Color
HARMONY is a state recognized by great philosophers as the immediate prerequisite of beauty. A compound is termed beautiful only when its parts are in harmonious combination. The world is called beautiful and its Creator is designated the Good because good perforce must act in conformity with its own nature; and good acting according to its own nature is harmony, because the good which it accomplishes is harmonious with the good which it is. Beauty, therefore, is harmony manifesting its own intrinsic nature in the world of form.
The universe is made up of successive gradations of good, these gradations ascending from matter (which is the least degree of good) to spirit (which is the greatest degree of good). In man, his superior nature is the summum bonum. It therefore follows that his highest nature most readily cognizes good because the good external to him in the world is in harmonic ratio with the good present in his soul. What man terms evil is therefore, in common with matter, merely the least degree of its own opposite. The least degree of good presupposes likewise the least degree of harmony and beauty. Thus deformity (evil) is really the least harmonious combination of elements naturally harmonic as individual units. Deformity is unnatural, for, the sum of all things being the Good, it is natural that all things should partake of the Good and be arranged in combinations that are harmonious. Harmony is the manifesting expression of the Will of the eternal Good.
THE PHILOSOPHY OF MUSIC
It is highly probable that the Greek initiates gained their knowledge of the philosophic and therapeutic aspects of music from the Egyptians, who, in turn, considered Hermes the founder of the art. According to one legend, this god constructed the first lyre by stretching strings across the concavity of a turtle shell. Both Isis and Osiris were patrons of music and poetry. Plato, in describing the antiquity of these arts among the Egyptians, declared that songs and poetry had existed in Egypt for at least ten thousand years, and that these were of such an exalted and inspiring nature that only gods or godlike men could have composed them. In the Mysteries the lyre was regarded as the secret symbol of the human constitution, the body of the instrument representing the physical form, the strings the nerves, and the musician the spirit. Playing upon the nerves, the spirit thus created the harmonies of normal functioning, which, however, became discords if the nature of man were defiled.
While the early Chinese, Hindus, Persians, Egyptians, Israelites, and Greeks employed both vocal and instrumental music in their religious ceremonials, also to complement their poetry and drama, it remained for Pythagoras to raise the art to its true dignity by demonstrating its mathematical foundation. Although it is said that he himself was not a musician, Pythagoras is now generally credited with the discovery of the diatonic scale. Having first learned the divine theory of music from the priests of the various Mysteries into which he had been accepted, Pythagoras pondered for several years upon the laws governing consonance and dissonance. How he actually solved the problem is unknown, but the following explanation has been invented.
One day while meditating upon the problem of harmony, Pythagoras chanced to pass a brazier's shop where workmen were pounding out a piece of metal upon an anvil. By noting the variances in pitch between the sounds made by large hammers and those made by smaller implements, and carefully estimating the harmonies and discords resulting from combinations of these sounds, he gained his first clue to the musical intervals of the diatonic scale. He entered the shop, and after carefully examining the tools and making mental note of their weights, returned to his own house and constructed an arm of wood so that it: extended out from the wall of his room. At regular intervals along this arm he attached four cords, all of like composition, size, and weight. To the first of these he attached a twelve-pound weight, to the second a nine-pound weight, to the third an eight-pound weight, and to the fourth a six-pound weight. These different weights corresponded to the sizes of the braziers' hammers.
Pythagoras thereupon discovered that the first and fourth strings when sounded together produced the harmonic interval of the octave, for doubling the weight had the same effect as halving the string. The tension of the first string being twice that of the fourth string, their ratio was said to be 2:1, or duple. By similar experimentation he ascertained that the first and third string produced the harmony of the diapente, or the interval of the fifth. The tension of the first string being half again as much as that of the third string, their ratio was said to be 3:2, or sesquialter. Likewise the second and fourth strings, having the same ratio as the first and third strings, yielded a diapente harmony. Continuing his investigation, Pythagoras discovered that the first and second strings produced the harmony of the diatessaron, or the interval of the third; and the tension of the first string being a third greater than that of the second string, their ratio was said to be 4:3, or sesquitercian. The third and fourth strings, having the same ratio as the first and second strings, produced another harmony of the diatessaron. According to Iamblichus, the second and third strings had the ratio of 8:9, or epogdoan.
The key to harmonic ratios is hidden in the famous Pythagorean tetractys, or pyramid of dots. The tetractys is made up of the first four numbers--1, 2, 3, and 4--which in their proportions reveal the intervals of the octave, the diapente, and the diatessaron. While the law of harmonic intervals as set forth above is true, it has been subsequently proved that hammers striking metal in the manner
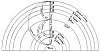
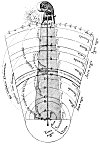
THE INTERVALS AND HARMONIES OF THE SPHERES.
From Stanley's The History of Philosophy.
In the Pythagorean concept of the music of the spheres, the interval between the earth and the sphere of the fixed stars was considered to be a diapason--the most perfect harmonic interval. The allowing arrangement is most generally accepted for the musical intervals of the planets between the earth and the sphere of the fixed stars: From the sphere of the earth to the sphere of the moon; one tone; from the sphere of the moon to that of Mercury, one half-tone; from Mercury to Venus, one-half; from Venus to the sun, one and one-half tones; from the sun to Mars, one tone; from Mars to Jupiter, one-half tone; from Jupiter to Saturn, one-half tone; from Saturn to the fixed stars, one-half tone. The sum of these intervals equals the six whole tones of the octave.
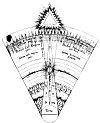
THE CONSONANCES OF THE MUNDANE MONOCHORD.
From Fludd's De Musica Mundana.
This diagrammatic sector represents the major gradations of energy and substance between elemental earth and absolute unconditioned force. Beginning with the superior, the fifteen graduated spheres descend in the following order: Limitless and Eternal Life; the superior, the middle, and the inferior Empyrean; the seven planets; and the four elements. Energy is symbolized by Fludd as a pyramid with its base upon the concave surface of the superior Empyrean, and substance as another Pyramid with its base upon the convex surface of the sphere (not planet) of earth. These pyramids demonstrate the relative proportions of energy and substance entering into the composition of the fifteen planes of being. It will be noted that the ascending pyramid of substance touches but does not pierce the fifteenth sphere--that of Limitless and Eternal Life. Likewise, the descending pyramid of energy touches but does not pierce the first sphere--the grossest condition of substance. The plane of the sun is denominated the sphere of equality, for here neither energy nor substance predominate. The mundane monochord consists of a hypothetical string stretched from the base of the pyramid of energy to the base of the pyramid of substance.
described will not produce the various tones ascribed to them. In all probability, therefore, Pythagoras actually worked out his theory of harmony from the monochord--a contrivance consisting of a single string stretched between two pegs and supplied with movable frets.
To Pythagoras music was one of the dependencies of the divine science of mathematics, and its harmonies were inflexibly controlled by mathematical proportions. The Pythagoreans averred that mathematics demonstrated the exact method by which the good established and maintained its universe. Number therefore preceded harmony, since it was the immutable law that governs all harmonic proportions. After discovering these harmonic ratios, Pythagoras gradually initiated his disciples into this, the supreme arcanum of his Mysteries. He divided the multitudinous parts of creation into a vast number of planes or spheres, to each of which he assigned a tone, a harmonic interval, a number, a name, a color, and a form. He then proceeded to prove the accuracy of his deductions by demonstrating them upon the different planes of intelligence and substance ranging from the most abstract logical premise to the most concrete geometrical solid. From the common agreement of these diversified methods of proof he established the indisputable existence of certain natural laws.
Having once established music as an exact science, Pythagoras applied his newly found law of harmonic intervals to all the phenomena of Nature, even going so far as to demonstrate the harmonic relationship of the planets, constellations, and elements to each other. A notable example of modern corroboration of ancient philosophical reaching is that of the progression of the elements according to harmonic ratios. While making a list of the elements in the ascending order of their atomic weights, John A. Newlands discovered at every eighth element a distinct repetition of properties. This discovery is known as the law of octaves in modern chemistry.
Since they held that harmony must be determined not by the sense perceptions but by reason and mathematics, the Pythagoreans called themselves Canonics, as distinguished from musicians of the Harmonic School, who asserted taste and instinct to be the true normative principles of harmony. Recognizing, however, the profound effect: of music upon the senses and emotions, Pythagoras did not hesitate to influence the mind and body with what he termed "musical medicine."
Pythagoras evinced such a marked preference for stringed instruments that he even went so far as to warn his disciples against allowing their ears to be defiled by the sounds of flutes or cymbals. He further declared that the soul could be purified from its irrational influences by solemn songs sung to the accompaniment of the lyre. In his investigation of the therapeutic value of harmonics, Pythagoras discovered that the seven modes--or keys--of the Greek system of music had the power to incite or allay the various emotions. It is related that while observing the stars one night he encountered a young man befuddled with strong drink and mad with jealousy who was piling faggots about his mistress' door with the intention of burning the house. The frenzy of the youth was accentuated by a flutist a short distance away who was playing a tune in the stirring Phrygian mode. Pythagoras induced the musician to change his air to the slow, and rhythmic Spondaic mode, whereupon the intoxicated youth immediately became composed and, gathering up his bundles of wood, returned quietly to his own home.
There is also an account of how Empedocles, a disciple of Pythagoras, by quickly changing the mode of a musical composition he was playing, saved the life of his host, Anchitus, when the latter was threatened with death by the sword of one whose father he had condemned to public execution. It is also known that Esculapius, the Greek physician, cured sciatica and other diseases of the nerves by blowing a loud trumpet in the presence of the patient.
Pythagoras cured many ailments of the spirit, soul, and body by having certain specially prepared musical compositions played in the presence of the sufferer or by personally reciting short selections from such early poets as Hesiod and Homer. In his university at Crotona it was customary for the Pythagoreans to open and to close each day with songs--those in the morning calculated to clear the mind from sleep and inspire it to the activities of the coming day; those in the evening of a mode soothing, relaxing, and conducive to rest. At the vernal equinox, Pythagoras caused his disciples to gather in a circle around one of their number who led them in song and played their accompaniment upon a lyre.
The therapeutic music of Pythagoras is described by Iamblichus thus: "And there are certain melodies devised as remedies against the passions of the soul, and also against despondency and lamentation, which Pythagoras invented as things that afford the greatest assistance in these maladies. And again, he employed other melodies against rage and anger, and against every aberration of the soul. There is also another kind of modulation invented as a remedy against desires." (See The Life of Pythagoras.)
It is probable that the Pythagoreans recognized a connection between the seven Greek modes and the planets. As an example, Pliny declares that Saturn moves in the Dorian mode and Jupiter in the Phrygian mode. It is also apparent that the temperaments are keyed to the various modes, and the passions likewise. Thus, anger--which is a fiery passion--may be accentuated by a fiery mode or its power neutralized by a watery mode.
The far-reaching effect exercised by music upon the culture of the Greeks is thus summed up by Emil Nauman: "Plato depreciated the notion that music was intended solely to create cheerful and agreeable emotions, maintaining rather that it should inculcate a love of all that is noble, and hatred of all that is mean, and that nothing could more strongly influence man's innermost feelings than melody and rhythm. Firmly convinced of this, he agreed with Damon of Athens, the musical instructor of Socrates, that the introduction of a new and presumably enervating scale would endanger the future of a whole nation, and that it was not possible to alter a key without shaking the very foundations of the State. Plato affirmed that music which ennobled the mind was of a far higher kind than that which merely appealed to the senses, and he strongly insisted that it was the paramount duty of the Legislature to suppress all music of an effeminate and lascivious character, and to encourage only s that which was pure and dignified; that bold and stirring melodies were for men, gentle and soothing ones for women. From this it is evident that music played a considerable part in the education of the Greek youth. The greatest care was also to be taken in the selection of instrumental music, because the absence of words rendered its signification doubtful, and it was difficult to foresee whether it would exercise upon the people a benign or baneful influence. Popular taste, being always tickled by sensuous and meretricious effects, was to be treated with deserved contempt. (See The History of Music.)
Even today martial music is used with telling effect in times of war, and religious music, while no longer developed in accordance with the ancient theory, still profoundly influences the emotions of the laity.
THE MUSIC OF THE SPHERES
The most sublime but least known of all the Pythagorean speculations was that of sidereal harmonics. It was said that of all men only Pythagoras heard the music of the spheres. Apparently the Chaldeans were the first people to conceive of the heavenly bodies joining in a cosmic chant as they moved in stately manner across the sky. Job describes a time "when the stars of the morning sang together," and in The Merchant of Venice the author of the Shakesperian plays
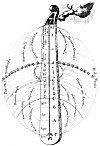
THE MUNDANE MONOCHORD WITH ITS PROPORTIONS AND INTERVALS.
From Fludd's De Musica Mundana.
In this chart is set forth a summary of Fludd's theory of universal music. The interval between the element of earth and the highest heaven is considered as a double octave, thus showing the two extremes of existence to be in disdiapason harmony. It is signifies that the highest heaven, the sun, and the earth have the same time, the difference being in pitch. The sun is the lower octave of the highest heaven and the earth the lower octave of the sun. The lower octave (Γ to G) comprises that part of the universe in which substance predominate over energy. Its harmonies, therefore, are more gross than those of the higher octave (G to g) wherein energy predominates over substance. "If struck in the more spiritual part," writes Fludd, "the monochord will give eternal life; if in the more material part, transitory life." It will be noted that certain elements, planets, and celestial spheres sustain a harmonic ratio to each other, Fludd advanced this as a key to the sympathies and antipathies existing between the various departments of Nature.
writes: "There's not the smallest orb which thou behold'st but in his motion like an angel sings." So little remains, however, of the Pythagorean system of celestial music that it is only possible to approximate his actual theory.
Pythagoras conceived the universe to be an immense monochord, with its single string connected at its upper end to absolute spirit and at its lower end to absolute matter--in other words, a cord stretched between heaven and earth. Counting inward from the circumference of the heavens, Pythagoras, according to some authorities, divided the universe into nine parts; according to others, into twelve parts. The twelvefold system was as follows: The first division was called the empyrean, or the sphere of the fixed stars, and was the dwelling place of the immortals. The second to twelfth divisions were (in order) the spheres of Saturn, Jupiter, Mars, the sun, Venus, Mercury, and the moon, and fire, air, water, and earth. This arrangement of the seven planets (the sun and moon being regarded as planets in the old astronomy) is identical with the candlestick symbolism of the Jews--the sun in the center as the main stem with three planets on either side of it.
The names given by the Pythagoreans to the various notes of the diatonic scale were, according to Macrobius, derived from an estimation of the velocity and magnitude of the planetary bodies. Each of these gigantic spheres as it rushed endlessly through space was believed to sound a certain tone caused by its continuous displacement of the Šthereal diffusion. As these tones were a manifestation of divine order and motion, it must necessarily follow that they partook of the harmony of their own source. "The assertion that the planets in their revolutions round the earth uttered certain sounds differing according to their respective 'magnitude, celerity and local distance,' was commonly made by the Greeks. Thus Saturn, the farthest planet, was said to give the gravest note, while the Moon, which is the nearest, gave the sharpest. 'These sounds of the seven planets, and the sphere of the fixed stars, together with that above us [Antichthon], are the nine Muses, and their joint symphony is called Mnemosyne.'" (See The Canon.)This quotation contains an obscure reference to the ninefold division of the universe previously mentioned.
The Greek initiates also recognized a fundamental relationship between the individual heavens or spheres of the seven planets, and the seven sacred vowels. The first heaven uttered the sound of the sacred vowel Α (Alpha); the second heaven, the sacred vowel Ε (Epsilon); the third, Η (Eta); the fourth, Ι (Iota); the fifth, Ο (Omicron); the sixth, Υ (Upsilon); and the seventh heaven, the sacred vowel Ω (Omega). When these seven heavens sing together they produce a perfect harmony which ascends as an everlasting praise to the throne of the Creator. (See IrenŠus' Against Heresies.) Although not so stated, it is probable that the planetary heavens are to be considered as ascending in the Pythagorean order, beginning with the sphere of the moon, which would be the first heaven.
Many early instruments had seven Strings, and it is generally conceded that Pythagoras was the one who added the eighth string to the lyre of Terpander. The seven strings were always related both to their correspondences in the human body and to the planets. The names of God were also conceived to be formed from combinations of the seven planetary harmonies. The Egyptians confined their sacred songs to the seven primary sounds, forbidding any others to be uttered in their temples. One of their hymns contained the following invocation: "The seven sounding tones praise Thee, the Great God, the ceaseless working Father of the whole universe." In another the Deity describes Himself thus: "I am the great indestructible lyre of the whole world, attuning the songs of the heavens. (See Nauman's History of Music.)
The Pythagoreans believed that everything which existed had a voice and that all creatures were eternally singing the praise of the Creator. Man fails to hear these divine melodies because his soul is enmeshed in the illusion of material existence. When he liberates himself from the bondage of the lower world with its sense limitations, the music of the spheres will again be audible as it was in the Golden Age. Harmony recognizes harmony, and when the human soul regains its true estate it will not only hear the celestial choir but also join with it in an everlasting anthem of praise to that Eternal Good controlling the infinite number of parts and conditions of Being.
The Greek Mysteries included in their doctrines a magnificent concept of the relationship existing between music and form. The elements of architecture, for example, were considered as comparable to musical modes and notes, or as having a musical counterpart. Consequently when a building was erected in which a number of these elements were combined, the structure was then likened to a musical chord, which was harmonic only when it fully satisfied the mathematical requirements of harmonic intervals. The realization of this analogy between sound and form led Goethe to declare that "architecture is crystallized music."
In constructing their temples of initiation, the early priests frequently demonstrated their superior knowledge of the principles underlying the phenomena known as vibration. A considerable part of the Mystery rituals consisted of invocations and intonements, for which purpose special sound chambers were constructed. A word whispered in one of these apartments was so intensified that the reverberations made the entire building sway and be filled with a deafening roar. The very wood and stone used in the erection of these sacred buildings eventually became so thoroughly permeated with the sound vibrations of the religious ceremonies that when struck they would reproduce the same tones thus repeatedly impressed into their substances by the rituals.
Every element in Nature has its individual keynote. If these elements are combined in a composite structure the result is a chord that, if sounded, will disintegrate the compound into its integral parts. Likewise each individual has a keynote that, if sounded, will destroy him. The allegory of the walls of Jericho falling when the trumpets of Israel were sounded is undoubtedly intended to set forth the arcane significance of individual keynote or vibration.
THE PHILOSOPHY OF COLOR
"Light," writes Edwin D. Babbitt, "reveals the glories of the external world and yet is the most glorious of them all. It gives beauty, reveals beauty and is itself most beautiful. It is the analyzer, the truth-teller and the exposer of shams, for it shows things as they are. Its infinite streams measure off the universe and flow into our telescopes from stars which are quintillions of miles distant. On the other hand it descends to objects inconceivably small, and reveals through the microscope objects fifty millions of times less than can be seen by the naked eye. Like all other fine forces, its movement is wonderfully soft, yet penetrating and powerful. Without its vivifying influence, vegetable, animal, and human life must immediately perish from the earth, and general ruin take place. We shall do well, then, to consider this potential and beautiful principle of light and its component colors, for the more deeply we penetrate into its inner laws, the more will it present itself as a marvelous storehouse of power to vitalize, heal, refine, and delight mankind." (See The Principles of Light and Color.)
Since light is the basic physical manifestation of life, bathing all creation in its radiance, it is highly important to realize, in part at least, the subtle nature of this divine substance. That which is called light is actually a rate of vibration causing certain reactions upon the optic nerve. Few realize how they are walled in by the limitations
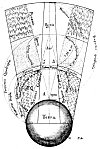
THE THEORY OF ELEMENTAL MUSIC.
From Fludd's De Musica Mundana.
In this diagram two interpenetrating pyramids are again employed, one of which represents fire and the other earth. It is demonstrated according to the law of elemental harmony that fire does not enter into the composition of earth nor earth into the composition of fire. The figures on the chart disclose the harmonic relationships existing between the four primary elements according to both Fludd and the Pythagoreans. Earth consists of four parts of its own nature; water of three parts of earth and one part of fire. The sphere of equality is a hypothetical point where there is an equilibrium of two parts of earth and two parts of fire. Air is composed of three parts of fire and one part of earth; fire, of four parts of its own nature. Thus earth and water bear to each other the ratio of 4 to 3, or the diatessaron harmony, and water and the sphere of equality the ratio of 3 to 2, or the diapente harmony. Fire and air also bear to each other the ratio of 4 to 3, or the diatessaron harmony, and air and the sphere of equality the ratio of 3 to 2, or the diapente harmony. As the sum of a diatessaron and a diapente equals a diapason, or octave, it is evident that both the sphere of fire and the sphere of earth are in diapason harmony with the sphere of equality, and also that fire and earth are in disdiapason harmony with each other.
of the sense perceptions. Not only is there a great deal more to light than anyone has ever seen but there are also unknown forms of light which no optical equipment will ever register. There are unnumbered colors which cannot be seen, as well as sounds which cannot be heard, odors which cannot be smelt, flavors which cannot be tasted, and substances which cannot be felt. Man is thus surrounded by a supersensible universe of which he knows nothing because the centers of sense perception within himself have not been developed sufficiently to respond to the subtler rates of vibration of which that universe is composed.
Among both civilized and savage peoples color has been accepted as a natural language in which to couch their religious and philosophical doctrines. The ancient city of Ecbatana as described by Herodotus, its seven walls colored according to the seven planets, revealed the knowledge of this subject possessed by the Persian Magi. The famous zikkurat or astronomical tower of the god Nebo at Borsippa ascended in seven great steps or stages, each step being painted in the key color of one of the planetary bodies. (See Lenormant's Chaldean Magic.) It is thus evident that the Babylonians were familiar with the concept of the spectrum in its relation to the seven Creative Gods or Powers. In India, one of the Mogul emperors caused a fountain to be made with seven levels. The water pouring down the sides through specially arranged channels changed color as it descended, passing sequentially through all shades of the spectrum. In Tibet, color is employed by the native artists to express various moods. L. Austine Waddell, writing of Northern Buddhist art, notes that in Tibetan mythology "White and yellow complexions usually typify mild moods, while the red, blue, and black belong to fierce forms, though sometimes light blue, as indicating the sky, means merely celestial. Generally the gods are pictured white, goblins red, and devils black, like their European relative." (See The Buddhism of Tibet.)
In Meno, Plato, speaking through Socrates, describes color as "an effluence of form, commensurate with sight, and sensible." In TheŠtetus he discourses more at length on the subject thus: "Let us carry out the principle which has just been affirmed, that nothing is self-existent, and then we shall see that every color, white, black, and every other color, arises out of the eye meeting the appropriate motion, and that what we term the substance of each color is neither the active nor the passive element, but something which passes between them, and is peculiar to each percipient; are you certain that the several colors appear to every animal--say a dog--as they appear to you?"
In the Pythagorean tetractys--the supreme symbol of universal forces and processes--are set forth the theories of the Greeks concerning color and music. The first three dots represent the threefold White Light, which is the Godhead containing potentially all sound and color. The remaining seven dots are the colors of the spectrum and the notes of the musical scale. The colors and tones are the active creative powers which, emanating from the First Cause, establish the universe. The seven are divided into two groups, one containing three powers and the other four a relationship also shown in the tetractys. The higher group--that of three--becomes the spiritual nature of the created universe; the lower group--that of four--manifests as the irrational sphere, or inferior world.
In the Mysteries the seven Logi, or Creative Lords, are shown as streams of force issuing from the mouth of the Eternal One. This signifies the spectrum being extracted from the white light of the Supreme Deity. The seven Creators, or Fabricators, of the inferior spheres were called by the Jews the Elohim. By the Egyptians they were referred to as the Builders (sometimes as the Governors) and are depicted with great knives in their hands with which they carved the universe from its primordial substance. Worship of the planets is based upon their acceptation as the cosmic embodiments of the seven creative attributes of God. The Lords of the planets were described as dwelling within the body of the sun, for the true nature of the sun, being analogous to the white light, contains the seeds of all the tone and color potencies which it manifests.
There are numerous arbitrary arrangements setting forth the mutual relationships of the planets, the colors, and the musical notes. The most satisfactory system is that based upon the law of the octave. The sense of hearing has a much wider scope than that of sight, for whereas the ear can register from nine to eleven octaves of sound the eye is restricted to the cognition of but seven fundamental color tones, or one tone short of the octave. Red, when posited as the lowest color tone in the scale of chromatics, thus corresponds to do, the first note of the musical scale. Continuing the analogy, orange corresponds to re, yellow to mi, green to fa, blue to sol, indigo to la, and violet to si (ti). The eighth color tone necessary to complete the scale should be the higher octave of red, the first color tone. The accuracy of the above arrangement is attested by two striking facts: (1) the three fundamental notes of the musical scale--the first, the third, and the fifth--correspond with the three primary colors--red, yellow, and blue; (2) the seventh, and least perfect, note of the musical scale corresponds with purple, the least perfect tone of the color scale.
In The Principles of Light and Color, Edwin D. Babbitt confirms the correspondence of the color and musical scales: "As C is at the bottom of the musical scale and made with the coarsest waves of air, so is red at the bottom of the chromatic scale and made with the coarsest waves of luminous ether. As the musical note B [the seventh note of the scale] requires 45 vibrations of air every time the note C at the lower end of the scale requires 24, or but little over half as many, so does extreme violet require about 300 trillions of vibrations of ether in a second, while extreme red requires only about 450 trillions, which also are but little more than half as many. When one musical octave is finished another one commences and progresses with just twice as many vibrations as were used in the first octave, and so the same notes are repeated on a finer scale. In the same way when the scale of colors visible to the ordinary eye is completed in the violet, another octave of finer invisible colors, with just twice as many vibrations, will commence and progress on precisely the same law."
When the colors are related to the twelve signs of the zodiac, they are arranged as the spokes of a wheel. To Aries is assigned pure red; to Taurus, red-orange; to Gemini, pure orange; to Cancer, orange-yellow; to Leo, pure yellow; to Virgo, yellow-green; to Libra, pure green; to Scorpio, green-blue; to Sagittarius, pure blue; to Capricorn, blue-violet; to Aquarius, pure violet; and to Pisces, violet-red.
In expounding the Eastern system of esoteric philosophy, H. P, Blavatsky relates the colors to the septenary constitution of man and the seven states of matter as follows:
COLOR
PRINCIPLES OF MAN
STATES OF MATTER
Violet
Chaya, or Etheric Double
Ether
Indigo
Higher Manas, or Spiritual Intelligence
Critical State called Air
Blue
Auric Envelope
Steam or Vapor
Green
Lower Manas, or Animal Soul
Critical State
Yellow
Buddhi, or Spiritual Soul
Water
Orange
Prana, or Life Principle
Critical State
Red
Kama Rupa, or Seat of Animal Life
Ice
This arrangement of the colors of the spectrum and the musical notes of the octave necessitates a different grouping of the planets in order to preserve their proper tone and color analogies. Thus do becomes Mars; re, the sun; mi, Mercury; fa, Saturn; sol, Jupiter; la, Venus; si (ti) the moon. (See The E. S. Instructions.)
THE FOUR ELEMENTS AND THEIR CONSONANTAL INTERVALS.
From Fludd's De Musica Mundana.
In this diagram Fludd has divided each of the four Primary elements into three subdivisions. The first division of each element is the grossest, partaking somewhat of the substance directly inferior to itself (except in the case of the earth, which has no state inferior to itself). The second division consists of the element in its relatively pure state, while the third division is that condition wherein the element partakes somewhat of the substance immediately superior to itself. For example the lowest division of the element of water is sedimentary, as it contains earth substance in solution; the second division represents water in its most common state--salty--as in the case of the ocean; and the third division is water in its purest state--free from salt. The harmonic interval assigned to the lowest division of each element is one tone, to the central division also a tone, but to the higher division a half-tone because it partakes of the division immediately above it. Fludd emphasizes the fact that as the elements ascend in series of two and a half tones, the diatessaron is the dominating harmonic interval of the elements.
Next: Fishes, Insects, Animals, Reptiles and Birds (Part One)